Model bodies and constraints for a HAWT
In this section we describe out approach to modeling a HAWT, including
the specific “bodies” that include massless nodes with six DOF (position
and orientation), 6-DOF rigid bodies, rigid connections, and flexible
beams. In the model descirbed here, the tower and blades are flexible
beams, with all other components being rigid.
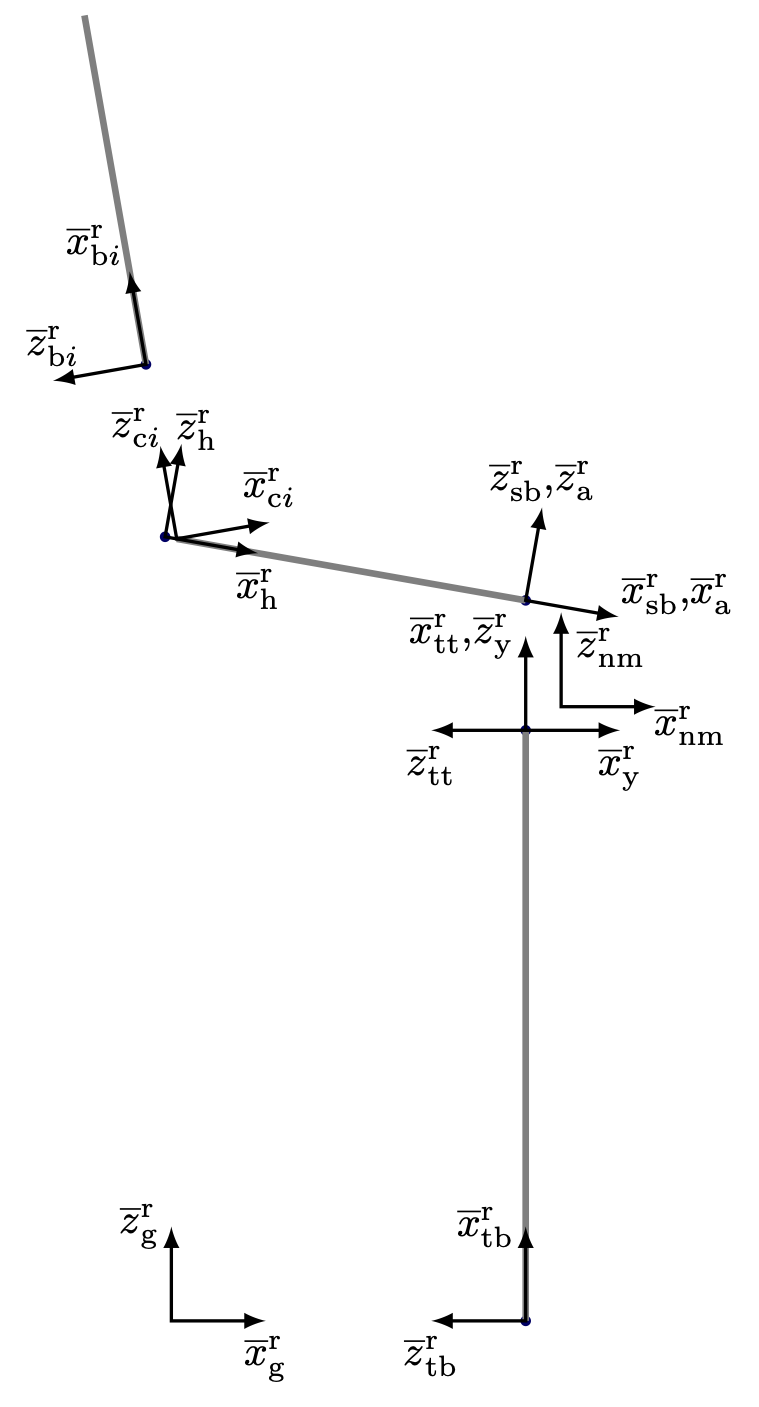
Table 1 defines the subscripts associated with
coordinate systems used to define the model, which are illustrated in
Figure 1. For example, the tower top is defined by
\(\underline{x}^\mathrm{r}_\mathrm{tt}\), \(\underline{u}_\mathrm{tt}\),
\(\underline{\underline{R}}^\mathrm{r}_\mathrm{tt}\), and
\(\underline{\underline{R}}_\mathrm{tt}\), which is the reference
position, displacement, reference orientation, and relative rotation,
respectively. The current orientation, denoted by a c-superscript, is
\(\underline{\underline{R}}^\mathrm{c}_\mathrm{tt} = \underline{\underline{R}}_\mathrm{tt} \underline{\underline{R}}^\mathrm{r}_\mathrm{tt}\).
subscript |
description |
|---|
g |
global/inertial |
tb |
tower base; first node in tower finite element |
tt |
tower top; last node in tower finite element |
yb |
yaw-base; bearing center of mass |
sb |
shaft base (does not rotate with rotor) |
a |
azimuth (rotates with rotor) |
h |
hub center of mass (rotates with rotor) |
c\(i\) |
coned CS for blade \(i\) (rotates with rotor;
does not pitch) |
b\(i\) |
blade CS for blade \(i\) (rotates with rotor;
pitches) |
nm |
Nacelle center of mass |
Constraints
In this section we define the constraints for our HAWT model. We start
at the base and move up through the connections. We assume the tower
base is fixed, for which the constraints can be written
(12)\[\begin{split}\underline{\Phi}_\mathrm{tb} =
\begin{bmatrix}
\underline{u}_\mathrm{tb}
\\ \mathrm{axial}\left({ \underline{\underline{R}}_\mathrm{tb} }\right)
\end{bmatrix}\end{split}\]
\(\underline{\Phi}_\mathrm{tb} \in \mathbb{R}^6\), where we have
used the axial vector to enforce zero rotation following
[@Sonneville-Bruls:2012]. The tower is represented by a flexible beam.
The constraint between the tower top and the yaw base is complicated by
the yaw controller and the motion of the beam model for the tower top.
We apply the yaw controller to the yaw base plate in the reference
configuration, resulting in the total rotation for the yaw:
\[\underline{\underline{R}}^\mathrm{c}_\mathrm{yb} = \underline{\underline{R}}_\mathrm{tt} \underline{\underline{R}}_\mathrm{yc} \underline{\underline{R}}_\mathrm{yb}^\mathrm{r}\]
which can be written
\[\underline{\underline{R}}_\mathrm{yb} \underline{\underline{R}}_\mathrm{yb}^\mathrm{r} = \underline{\underline{R}}_\mathrm{tt} \underline{\underline{R}}_\mathrm{yc} \underline{\underline{R}}_\mathrm{yb}^\mathrm{r}\]
and simplified to
\[\underline{\underline{R}}_\mathrm{yb} = \underline{\underline{R}}_\mathrm{tt} \underline{\underline{R}}_\mathrm{yc},\]
Keeping the yaw displacement tied to tower top displacement, the
constraints between the tower-top and yaw baseplate are
\[\begin{split}\underline{\Phi}_\mathrm{yb-tt} =
\begin{Bmatrix}
\underline{u}_\mathrm{yb}
-\underline{u}_\mathrm{tt}
\\ \mathrm{axial}\left({ \underline{\underline{R}}_\mathrm{yb} \underline{\underline{R}}_\mathrm{yc}^T \underline{\underline{R}}_\mathrm{tt}^T }\right)
\end{Bmatrix}\end{split}\]
\(\underline{\Phi}_\mathrm{yb-tt} \in \mathbb{R}^6\).
The shaft base and yaw CS’s are assumed to be rigidly connected. Here,
shaft-base relative rotation is the same as the yaw relative rotation:
\[\begin{split}\underline{\Phi}_\mathrm{sb-yb} =
\begin{Bmatrix}
\underline{u}_\mathrm{sb} + \underline{x}^\mathrm{r}_\mathrm{sb} -\underline{u}_\mathrm{yb} -\underline{x}^\mathrm{r}_\mathrm{yb}
- \underline{\underline{R}}_\mathrm{yb} \left(\underline{x}^\mathrm{r}_\mathrm{sb}-\underline{x}^\mathrm{r}_\mathrm{yb}\right)
\\ \mathrm{axial}\left({ \underline{\underline{R}}_\mathrm{sb} \underline{\underline{R}}_\mathrm{yb}^T}\right)
\end{Bmatrix}\end{split}\]
\(\underline{\Phi}_\mathrm{sb-yb} \in \mathbb{R}^6\).
The azimuth CS is free to rotate about the
\(\widehat{x}_\mathrm{sb}\) axis and is tied to the location of the
shaft-base CS.
\[\begin{split}\underline{\Phi}_\mathrm{a-sb} =
\begin{Bmatrix}
\underline{u}_\mathrm{a}-\underline{u}_\mathrm{sb}
\\ \widehat{z}_\mathrm{a}^T \widehat{x}_\mathrm{sb} \\
\widehat{y}_\mathrm{a}^T \widehat{x}_\mathrm{sb}
\end{Bmatrix} =
\begin{Bmatrix}
\underline{u}_\mathrm{a}-\underline{u}_\mathrm{sb}
\\ \widehat{z}_\mathrm{a}^{\mathrm{r}T} \underline{\underline{R}}_\mathrm{a}^T \underline{\underline{R}}_\mathrm{sb} \widehat{x}_\mathrm{sb}^\mathrm{r} \\
\widehat{y}_\mathrm{a}^{\mathrm{r}T} \underline{\underline{R}}_\mathrm{a}^T \underline{\underline{R}}_\mathrm{sb} \widehat{x}_\mathrm{sb}^\mathrm{r}
\end{Bmatrix}\end{split}\]
\(\underline{\Phi}_\mathrm{a-sb} \in \mathbb{R}^5\).
The hub coordinate system (for a rigid shaft) has the same relative
rotation as the azimuth CS
\[\begin{split}\underline{\Phi}_\mathrm{h-a} =
\begin{Bmatrix}
\underline{u}_\mathrm{h}+\underline{x}^\mathrm{r}_\mathrm{h} -\underline{u}_\mathrm{a} - \underline{x}^\mathrm{r}_\mathrm{a}-
\underline{\underline{R}}_\mathrm{a} \left(\underline{x}^\mathrm{r}_\mathrm{h}-\underline{x}^\mathrm{r}_\mathrm{a}\right)
\\ \mathrm{axial}\left({ \underline{\underline{R}}_\mathrm{h} \underline{\underline{R}}_\mathrm{a}^T}\right)
\end{Bmatrix}\end{split}\]
\(\underline{\Phi}_\mathrm{h-a} \in \mathbb{R}^6\).
The cone CS for blade \(i\) rotates with the hub and the cone CS
displacement is equal to that of the hub, but does not pitch.
\[\begin{split}\underline{\Phi}_{\mathrm{c}i\mathrm{-h}} =
\begin{Bmatrix}
\underline{u}_{\mathrm{c}i}-\underline{u}_\mathrm{h}
\\ \mathrm{axial}\left({ \underline{\underline{R}}_{\mathrm{c}i} \underline{\underline{R}}_\mathrm{h}^T}\right)
\end{Bmatrix}\end{split}\]
\(\underline{\Phi}_{\mathrm{c}i-h} \in \mathbb{R}^6\).
The blade-root CS for blade \(i\) is offset from the cone CS and it
pitches.
\[\begin{split}\underline{\Phi}_{\mathrm{b}i-\mathrm{c}i} =
\begin{Bmatrix}
\underline{u}_{\mathrm{b}i} + \underline{x}^\mathrm{r}_{\mathrm{b}i}-\underline{u}_{\mathrm{c}i}
- \underline{x}^\mathrm{r}_{\mathrm{c}i}
- \underline{\underline{R}}_{\mathrm{c}i}\left(\underline{x}^\mathrm{r}_{\mathrm{b}i} - \underline{x}^\mathrm{r}_{\mathrm{c}i}\right)
\\ \mathrm{axial}\left({ \underline{\underline{R}}_{\mathrm{b}i} \underline{\underline{R}}_{\mathrm{pc}i}^T \underline{\underline{R}}_{\mathrm{c}i}^T }\right)
\end{Bmatrix}\end{split}\]
\(\underline{\Phi}_{\mathrm{b}i-h} \in \mathbb{R}^6\).
The nacelle-mass and yaw-base CS’s are assumed to be rigidly connected.
\[\begin{split}\underline{\Phi}_\mathrm{nm-yb} =
\begin{Bmatrix}
\underline{u}_\mathrm{nm} + \underline{x}^\mathrm{r}_\mathrm{nm} -\underline{u}_\mathrm{yb} -\underline{x}^\mathrm{r}_\mathrm{yb}
- \underline{\underline{R}}_\mathrm{yb} \left(\underline{x}^\mathrm{r}_\mathrm{nm}-\underline{x}^\mathrm{r}_\mathrm{yb}\right)
\\ \mathrm{axial}\left({ \underline{\underline{R}}_\mathrm{nm} \underline{\underline{R}}_\mathrm{yb}^T}\right)
\end{Bmatrix}\end{split}\]
\(\underline{\Phi}_\mathrm{nb-sb} \in \mathbb{R}^6\).
Constraint Gradient
In this section we derive the constraint gradient matrices associated
with each of the constraints defined in the previous section. Consider
the constraint given by Eq. (12), which
after taking the variation can be written
\[\begin{split}\underline{\underline{B}}_\mathrm{tb}
\begin{Bmatrix}
\delta \underline{u}_\mathrm{tb}\\
\underline{\delta \theta}_\mathrm{tb}
\end{Bmatrix}
= \begin{bmatrix}
\underline{\underline{I}} & \underline{\underline{0}} \\
\underline{\underline{0}} & \mathrm{AX}\left( \underline{\underline{R}}_\mathrm{tb} \right)
\end{bmatrix}
\begin{Bmatrix}
\delta \underline{u}_\mathrm{tb}\\
\underline{\delta \theta}_\mathrm{tb}
\end{Bmatrix}\end{split}\]
where we leveraged the following identity
\[\mathrm{axial}\left({ \underline{\underline{A}} \widetilde{a}}\right) = \frac{1}{2} \left(\mathrm{tr} \left( \underline{\underline{A^T}} \right) \underline{\underline{I}} - \underline{\underline{A}}^T \right) \underline{a}\]
and we introduced the operator
\[\mathrm{AX}\left( \underline{\underline{A}} \right) = \frac{1}{2} \left(\mathrm{tr} \left( \underline{\underline{A}} \right) \underline{\underline{I}} - \underline{\underline{A}} \right)\]
Proceeding in a similar fashion for the remaining contraints, we find
the following contraint gradient matrices:
\[\begin{split}\underline{\underline{B}}_\mathrm{yb-tt}
\begin{Bmatrix}
\delta \underline{u}_\mathrm{yb}\\
\underline{\delta \theta}_\mathrm{yb}\\
\delta \underline{u}_\mathrm{tt}\\
\underline{\delta \theta}_\mathrm{tt}
\end{Bmatrix}
= \begin{bmatrix}
\underline{\underline{I}} & \underline{\underline{0}} & -\underline{\underline{I}} & \underline{\underline{0}} \\
\underline{\underline{0}} & \mathrm{AX}\left( \underline{\underline{R}}_\mathrm{yb}
\underline{\underline{R}}_\mathrm{yc}^T
\underline{\underline{R}}_\mathrm{tt}^T \right) &
\underline{\underline{0}} & -\mathrm{AX}\left( \underline{\underline{R}}_\mathrm{tt}
\underline{\underline{R}}_\mathrm{yc}
\underline{\underline{R}}_\mathrm{yb}^T\right)
\end{bmatrix}
\begin{Bmatrix}
\delta \underline{u}_\mathrm{yb}\\
\underline{\delta \theta}_\mathrm{yb}\\
\delta \underline{u}_\mathrm{tt}\\
\underline{\delta \theta}_\mathrm{tt}
\end{Bmatrix}\end{split}\]
\[\begin{split}\underline{\underline{B}}_\mathrm{sb-yb}
\begin{Bmatrix}
\delta \underline{u}_\mathrm{sb}\\
\underline{\delta \theta}_\mathrm{sb}\\
\delta \underline{u}_\mathrm{yb}\\
\underline{\delta \theta}_\mathrm{yb}
\end{Bmatrix}
= \begin{bmatrix}
\underline{\underline{I}} & \underline{\underline{0}} & -\underline{\underline{I}} & \widetilde{\underline{\underline{R}}_\mathrm{yb}
\left( \underline{x}_\mathrm{sb}^\mathrm{r}-\underline{x}_\mathrm{yb}^\mathrm{r} \right)} \\
\underline{\underline{0}} & \mathrm{AX}\left( \underline{\underline{R}}_\mathrm{sb} \underline{\underline{R}}_\mathrm{yb}^T \right) &
\underline{\underline{0}} & -\mathrm{AX}\left( \underline{\underline{R}}_\mathrm{yb} \underline{\underline{R}}_\mathrm{sb}^T \right)
\end{bmatrix}
\begin{Bmatrix}
\delta \underline{u}_\mathrm{sb}\\
\underline{\delta \theta}_\mathrm{sb}\\
\delta \underline{u}_\mathrm{yb}\\
\underline{\delta \theta}_\mathrm{yb}
\end{Bmatrix}\end{split}\]
\[\begin{split}\underline{\underline{B}}_\mathrm{a-sb}
\begin{Bmatrix}
\delta \underline{u}_\mathrm{a}\\
\underline{\delta \theta}_\mathrm{a}\\
\delta \underline{u}_\mathrm{sb}\\
\underline{\delta \theta}_\mathrm{sb}
\end{Bmatrix}
= \begin{bmatrix}
\underline{\underline{I}} & \underline{\underline{0}} & -\underline{\underline{I}} & \underline{\underline{0}} \\
\underline{0}^T & \widehat{z}_\mathrm{a}^T \widetilde{x}_\mathrm{sb} &
\underline{0}^T & -\widehat{z}_\mathrm{a}^T \widetilde{x}_\mathrm{sb} \\
\underline{0}^T & \widehat{yb}_\mathrm{a}^T \widetilde{x}_\mathrm{sb} &
\underline{0}^T & -\widehat{yb}_\mathrm{a}^T \widetilde{x}_\mathrm{sb}
\end{bmatrix}
\begin{Bmatrix}
\delta \underline{u}_\mathrm{a}\\
\underline{\delta \theta}_\mathrm{a}\\
\delta \underline{u}_\mathrm{sb}\\
\underline{\delta \theta}_\mathrm{sb}
\end{Bmatrix}\end{split}\]
\[\begin{split}\underline{\underline{B}}_\mathrm{h-a}
\begin{Bmatrix}
\delta \underline{u}_\mathrm{h}\\
\underline{\delta \theta}_\mathrm{h}\\
\delta \underline{u}_\mathrm{a}\\
\underline{\delta \theta}_\mathrm{a}
\end{Bmatrix}
= \begin{bmatrix}
\underline{\underline{I}} & \underline{\underline{0}} & -\underline{\underline{I}} &
\widetilde{\underline{\underline{R}}_\mathrm{a}
\left( \underline{x}_\mathrm{h}^\mathrm{r}-\underline{x}_\mathrm{a}^\mathrm{r} \right)} \\
\underline{\underline{0}} & \mathrm{AX}\left( \underline{\underline{R}}_\mathrm{h} \underline{\underline{R}}_\mathrm{a}^T \right) &
\underline{\underline{0}} & -\mathrm{AX}\left( \underline{\underline{R}}_\mathrm{a} \underline{\underline{R}}_\mathrm{h}^T \right)
\end{bmatrix}
\begin{Bmatrix}
\delta \underline{u}_\mathrm{h}\\
\underline{\delta \theta}_\mathrm{h}\\
\delta \underline{u}_\mathrm{a}\\
\underline{\delta \theta}_\mathrm{a}
\end{Bmatrix}\end{split}\]
\[\begin{split}\underline{\underline{B}}_{\mathrm{c}i-\mathrm{h}}
\begin{Bmatrix}
\delta \underline{u}_{\mathrm{c}i}\\
\underline{\delta \theta}_{\mathrm{c}i}\\
\delta \underline{u}_\mathrm{h}\\
\underline{\delta \theta}_\mathrm{h}
\end{Bmatrix}
= \begin{bmatrix}
\underline{\underline{I}} & \underline{\underline{0}} & -\underline{\underline{I}} & \underline{\underline{0}} \\
\underline{\underline{0}} & \mathrm{AX}\left( \underline{\underline{R}}_{\mathrm{c}i} \underline{\underline{R}}_\mathrm{h}^T \right) &
\underline{\underline{0}} & -\mathrm{AX}\left( \underline{\underline{R}}_\mathrm{h} \underline{\underline{R}}_{\mathrm{c}i}^T \right)
\end{bmatrix}
\begin{Bmatrix}
\delta \underline{u}_{\mathrm{c}i}\\
\underline{\delta \theta}_{\mathrm{c}i}\\
\delta \underline{u}_\mathrm{h}\\
\underline{\delta \theta}_\mathrm{h}
\end{Bmatrix}\end{split}\]
\[\begin{split}\underline{\underline{B}}_{\mathrm{b}i-\mathrm{c}i}
\begin{Bmatrix}
\delta \underline{u}_{\mathrm{b}i}\\
\underline{\delta \theta}_{\mathrm{b}i}\\
\delta \underline{u}_{\mathrm{c}i}\\
\underline{\delta \theta}_{\mathrm{c}i}
\end{Bmatrix}
= \begin{bmatrix}
\underline{\underline{I}} & \underline{\underline{0}} & -\underline{\underline{I}} &
\widetilde{\underline{\underline{R}}_{\mathrm{c}i}
\left( \underline{x}_{\mathrm{b}i}^\mathrm{r}-\underline{x}_{\mathrm{c}i}^0 \right)} \\
\underline{\underline{0}} & \mathrm{AX}\left( \underline{\underline{R}}_{\mathrm{b}i}
\underline{\underline{R}}_{\mathrm{pc}i}^T
\underline{\underline{R}}_{\mathrm{c}i}^T \right) &
\underline{\underline{0}} & -\mathrm{AX}\left( \underline{\underline{R}}_{\mathrm{c}i}
\underline{\underline{R}}_{\mathrm{pc}i}
\underline{\underline{R}}_{\mathrm{b}i}^T\right)
\end{bmatrix}
\begin{Bmatrix}
\delta \underline{u}_{\mathrm{b}i}\\
\underline{\delta \theta}_{\mathrm{b}i}\\
\delta \underline{u}_{\mathrm{c}i}\\
\underline{\delta \theta}_{\mathrm{c}i}
\end{Bmatrix}\end{split}\]
\[\begin{split}\underline{\underline{B}}_\mathrm{nm-yb}
\begin{Bmatrix}
\delta \underline{u}_\mathrm{nm}\\
\underline{\delta \theta}_\mathrm{nm}\\
\delta \underline{u}_\mathrm{yb}\\
\underline{\delta \theta}_\mathrm{yb}
\end{Bmatrix}
= \begin{bmatrix}
\underline{\underline{I}} & \underline{\underline{0}} & -\underline{\underline{I}} & \widetilde{\underline{\underline{R}}_\mathrm{yb}
\left( \underline{x}_\mathrm{nm}^\mathrm{r}-\underline{x}_\mathrm{yb}^\mathrm{r} \right)} \\
\underline{\underline{0}} & \mathrm{AX}\left( \underline{\underline{R}}_\mathrm{nm} \underline{\underline{R}}_\mathrm{yb}^T \right) &
\underline{\underline{0}} & -\mathrm{AX}\left( \underline{\underline{R}}_\mathrm{yb} \underline{\underline{R}}_\mathrm{nm}^T \right)
\end{bmatrix}
\begin{Bmatrix}
\delta \underline{u}_\mathrm{nm}\\
\underline{\delta \theta}_\mathrm{nm}\\
\delta \underline{u}_\mathrm{yb}\\
\underline{\delta \theta}_\mathrm{yb}
\end{Bmatrix}\end{split}\]
Additional iteration matrix terms due to constraints
For a residual expressed as in Eq. (1),
there may be additional terms that arise in the
\(\underline{\underline{K}}^\Phi\) term in
Eq. (4) if the constraint-gradient
matrix is not constant with respect to the depdendent variables, e.g.,
\(\underline{\underline{B}}=\underline{\underline{B}}(\underline{q})\).
Consider, for example, \(\underline{\underline{B}}_\mathrm{tb}\),
for which the associated residual force can be written
\[\begin{aligned}
\underline{F}_\mathrm{tb}=\underline{\underline{B}}_\mathrm{tb}^T \underline{\lambda}_\mathrm{tb}
\end{aligned}\]
where
\(\underline{F}_\mathrm{tb}\,,\underline{\lambda}_\mathrm{tb} \in \mathbb{R}^6\).
Taking the variation we obtain
(13)\[\begin{split}\delta \underline{F}_\mathrm{tb}=
\underline{\underline{K}}_\mathrm{tb}^\Phi
\begin{bmatrix}
\delta \underline{u}_\mathrm{tb} \\
\delta \underline{\theta}_\mathrm{tb}
\end{bmatrix}
+ \underline{\underline{B}}_\mathrm{tb}^T \delta \underline{\lambda}_\mathrm{tb}\end{split}\]
where
\[\begin{split}\begin{aligned}
\underline{\underline{K}}_\mathrm{tb}^\Phi
\begin{bmatrix}
\delta \underline{u}_\mathrm{tb} \\
\delta \underline{\theta}_\mathrm{tb}
\end{bmatrix}
=
\begin{bmatrix}
\underline{\underline{0}} & \underline{\underline{0}} \\
\underline{\underline{0}} & \mathrm{AX} \left( - \underline{\underline{R}}_\mathrm{tb} \widetilde{ \lambda_{\mathrm{tb},2} } \right)
\end{bmatrix}
\begin{bmatrix}
\delta \underline{u}_\mathrm{tb} \\
\delta \underline{\theta}_\mathrm{tb}
\end{bmatrix}
\end{aligned}\end{split}\]
and
\[\begin{split}\begin{aligned}
\underline{\lambda}_\mathrm{tb} =
\begin{bmatrix}
\underline{\lambda}_{\mathrm{tb},1}\\
\underline{\lambda}_{\mathrm{tb},2}
\end{bmatrix}
\end{aligned}\end{split}\]
The \(\underline{\underline{B}}^T_\mathrm{tb}\) term in
Eq. (13) goes in the
appropriate location in the upper right quadrant of
Eq. (4) and the
\(\underline{\underline{K}}_\mathrm{tb}^\Phi\) term is added to the
\(\underline{\underline{K}}\) matrix in the upper left quadrant.
Proceeding in a similar fashion for the remaining constraint forces, we
find:
\[\begin{split}\begin{aligned}
\underline{\underline{K}}_\mathrm{yb-tt}^\Phi
\begin{bmatrix}
\delta \underline{u}_\mathrm{yb} \\
\delta \underline{\theta}_\mathrm{yb}\\
\delta \underline{u}_\mathrm{tt} \\
\delta \underline{\theta}_\mathrm{tt}
\end{bmatrix}
=
\begin{bmatrix}
\underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}}\\
\underline{\underline{0}} & \mathrm{AX} \left(\underline{\underline{R}}_\mathrm{yb} \underline{\underline{R}}_\mathrm{yc}^T \underline{\underline{R}}_\mathrm{tt}^T \widetilde{\lambda}_{\mathrm{yb-tt},2} \right) &
\underline{\underline{0}} & \mathrm{AX2}\left( \underline{\lambda}_{\mathrm{yb-tt},2}, \underline{\underline{R}}_\mathrm{tt} \underline{\underline{R}}_\mathrm{yc} \underline{\underline{R}}_\mathrm{yb}^T\right) \\
\underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}}\\
\underline{\underline{0}} & -\mathrm{AX2} \left( \underline{\lambda}_{\mathrm{yb-tt},2}, \underline{\underline{R}}_\mathrm{yb} \underline{\underline{R}}_\mathrm{yc}^T \underline{\underline{R}}_\mathrm{tt}^T\right)
& \underline{\underline{0}} & -\mathrm{AX} \left( \underline{\underline{R}}_\mathrm{tt} \underline{\underline{R}}_\mathrm{yc} \underline{\underline{R}}_\mathrm{yb}^T \widetilde{\lambda}_{\mathrm{yb-tt},2} \right) &
\end{bmatrix}
\begin{bmatrix}
\delta \underline{u}_\mathrm{yb} \\
\delta \underline{\theta}_\mathrm{yb}\\
\delta \underline{u}_\mathrm{tt} \\
\delta \underline{\theta}_\mathrm{tt}
\end{bmatrix}
\end{aligned}\end{split}\]
where
\[\begin{split}\begin{aligned}
\mathrm{AX2}\left(\underline{a},\underline{\underline{A}}\right) = \frac{1}{2}
\begin{bmatrix}
a_1 (A_{23}- A_{32}) & -a_1 A_{13}-a_2 A_{32}-a_3 A_{33} & a_1 A_{12}+a_2 A_{22} + a_3 A_{23} \\
a_2 A_{23} + a_1 A_{31} + a_3 A_{33} & a_2 (A_{31}-A_{13}) & -a_1 A_{11}-a_2 A_{21} - a_3 A_{13} \\
-a_1 A_{21}-a_2 A_{22}-a_3 A_{32} & a_1 A_{11}+a_2 A_{12}+a_3 A_{31} & a_3 (A_{12}-A_{21})
\end{bmatrix}
\end{aligned}\end{split}\]
\[\begin{split}\begin{aligned}
\underline{\underline{K}}_\mathrm{sb-yb}^\Phi
\begin{bmatrix}
\delta \underline{u}_\mathrm{sb} \\
\delta \underline{\theta}_\mathrm{sb}\\
\delta \underline{u}_\mathrm{yb} \\
\delta \underline{\theta}_\mathrm{yb}
\end{bmatrix}
=
\begin{bmatrix}
\underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}}\\
\underline{\underline{0}} & \mathrm{AX} \left(\underline{\underline{R}}_\mathrm{sb} \underline{\underline{R}}_\mathrm{yb}^T \widetilde{\lambda}_{\mathrm{sb-yb},2} \right) &
\underline{\underline{0}} & \mathrm{AX2}\left( \underline{\lambda}_{\mathrm{sb-yb},2}, \underline{\underline{R}}_\mathrm{yb} \underline{\underline{R}}_\mathrm{sb}^T\right) \\
\underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}}\\
\underline{\underline{0}} & -\mathrm{AX2} \left( \underline{\lambda}_{\mathrm{sb-yb},2}, \underline{\underline{R}}_\mathrm{sb} \underline{\underline{R}}_\mathrm{yb}^T\right)
& \underline{\underline{0}} & -\mathrm{AX} \left( \underline{\underline{R}}_\mathrm{yb} \underline{\underline{R}}_\mathrm{sb}^T \widetilde{\lambda}_{\mathrm{sb-yb},2} \right)
-\widetilde{\lambda}_\mathrm{sb-yb,1} \widetilde{ \underline{\underline{R}}_\mathrm{yb} \left( \underline{x}^\mathrm{r}_\mathrm{sb}-\underline{x}^\mathrm{r}_\mathrm{yb} \right) }
\end{bmatrix}
\begin{bmatrix}
\delta \underline{u}_\mathrm{sb} \\
\delta \underline{\theta}_\mathrm{sb}\\
\delta \underline{u}_\mathrm{yb} \\
\delta \underline{\theta}_\mathrm{yb}
\end{bmatrix}
\end{aligned}\end{split}\]
\[\begin{split}\begin{aligned}
\underline{\underline{K}}_\mathrm{a-sb}^\Phi
\begin{bmatrix}
\delta \underline{u}_\mathrm{a} \\
\delta \underline{\theta}_\mathrm{a}\\
\delta \underline{u}_\mathrm{sb} \\
\delta \underline{\theta}_\mathrm{sb}
\end{bmatrix}
=
\begin{bmatrix}
\underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}}\\
\underline{\underline{0}} & \lambda_\mathrm{a-sb,2} \widetilde{x}_\mathrm{sb} \widetilde{z}_\mathrm{a}
+ \lambda_\mathrm{a-sb,3} \widetilde{x}_\mathrm{sb} \widetilde{y}_\mathrm{a}
& \underline{\underline{0}} &
-\lambda_\mathrm{a-sb,2} \widetilde{z}_\mathrm{a} \widetilde{x}_\mathrm{sb}
- \lambda_\mathrm{a-sb,3} \widetilde{y}_\mathrm{a} \widetilde{x}_\mathrm{sb}
\\
\underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}}\\
\underline{\underline{0}} & -\lambda_\mathrm{a-sb,2} \widetilde{x}_\mathrm{sb} \widetilde{z}_\mathrm{a}
- \lambda_\mathrm{a-sb,3} \widetilde{x}_\mathrm{sb} \widetilde{y}_\mathrm{a}
& \underline{\underline{0}} &
\lambda_\mathrm{a-sb,2} \widetilde{z}_\mathrm{a} \widetilde{x}_\mathrm{sb}
+ \lambda_\mathrm{a-sb,3} \widetilde{y}_\mathrm{a} \widetilde{x}_\mathrm{sb}
\end{bmatrix}
\begin{bmatrix}
\delta \underline{u}_\mathrm{a} \\
\delta \underline{\theta}_\mathrm{a}\\
\delta \underline{u}_\mathrm{sb} \\
\delta \underline{\theta}_\mathrm{sb}
\end{bmatrix}
\end{aligned}\end{split}\]
where
\[\begin{split}\begin{aligned}
\lambda_\mathrm{a-sb} =
\begin{bmatrix}
\underline{\lambda}_\mathrm{a-sb,1} \\
\lambda_\mathrm{a-sb,2} \\
\lambda_\mathrm{a-sb,3} \\
\end{bmatrix} \in \mathbb{R}^5
\end{aligned}\end{split}\]
\[\begin{split}\begin{aligned}
\underline{\underline{K}}_\mathrm{h-a}^\Phi
\begin{bmatrix}
\delta \underline{u}_\mathrm{h} \\
\delta \underline{\theta}_\mathrm{h}\\
\delta \underline{u}_\mathrm{a} \\
\delta \underline{\theta}_\mathrm{a}
\end{bmatrix}
=
\begin{bmatrix}
\underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}}\\
\underline{\underline{0}} & \mathrm{AX} \left(\underline{\underline{R}}_\mathrm{h} \underline{\underline{R}}_\mathrm{a}^T \widetilde{\lambda}_{\mathrm{h-a},2} \right) &
\underline{\underline{0}} & \mathrm{AX2}\left( \underline{\lambda}_{\mathrm{h-a},2}, \underline{\underline{R}}_\mathrm{a} \underline{\underline{R}}_\mathrm{h}^T\right) \\
\underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}}\\
\underline{\underline{0}} & -\mathrm{AX2} \left( \underline{\lambda}_{\mathrm{h-a},2}, \underline{\underline{R}}_\mathrm{h} \underline{\underline{R}}_\mathrm{a}^T\right)
& \underline{\underline{0}} & -\mathrm{AX} \left( \underline{\underline{R}}_\mathrm{a} \underline{\underline{R}}_\mathrm{h}^T \widetilde{\lambda}_{\mathrm{h-a},2} \right)
-\widetilde{\lambda}_\mathrm{h-a,1} \widetilde{ \underline{\underline{R}}_\mathrm{a} \left( \underline{x}^\mathrm{r}_\mathrm{h}-\underline{x}^\mathrm{r}_\mathrm{a} \right) }
\end{bmatrix}
\begin{bmatrix}
\delta \underline{u}_\mathrm{h} \\
\delta \underline{\theta}_\mathrm{h}\\
\delta \underline{u}_\mathrm{a} \\
\delta \underline{\theta}_\mathrm{a}
\end{bmatrix}
\end{aligned}\end{split}\]
\[\begin{split}\begin{aligned}
\underline{\underline{K}}_{\mathrm{c}i\mathrm{-h}}^\Phi
\begin{bmatrix}
\delta \underline{u}_{\mathrm{c}i} \\
\delta \underline{\theta}_{\mathrm{c}i}\\
\delta \underline{u}_\mathrm{h} \\
\delta \underline{\theta}_\mathrm{h}
\end{bmatrix}
=
\begin{bmatrix}
\underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}}\\
\underline{\underline{0}} & \mathrm{AX} \left(\underline{\underline{R}}_{\mathrm{c}i} \underline{\underline{R}}_\mathrm{h}^T \widetilde{\lambda}_{\mathrm{c}i\mathrm{-h,2}} \right) &
\underline{\underline{0}} & \mathrm{AX2}\left(\underline{\lambda}_{\mathrm{c}i\mathrm{-h,2}}, \underline{\underline{R}}_\mathrm{h} \underline{\underline{R}}_{\mathrm{c}i}^T\right) \\
\underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}}\\
\underline{\underline{0}} & -\mathrm{AX2} \left( \underline{\lambda}_{\mathrm{c}i\mathrm{-h,2}}, \underline{\underline{R}}_{\mathrm{c}i} \underline{\underline{R}}_\mathrm{h}^T\right)
& \underline{\underline{0}} & -\mathrm{AX} \left( \underline{\underline{R}}_\mathrm{h} \underline{\underline{R}}_{\mathrm{c}i}^T \widetilde{\lambda}_{\mathrm{c}i\mathrm{-h,2}} \right)
\end{bmatrix}
\begin{bmatrix}
\delta \underline{u}_{\mathrm{c}i} \\
\delta \underline{\theta}_{\mathrm{c}i}\\
\delta \underline{u}_\mathrm{h} \\
\delta \underline{\theta}_\mathrm{h}
\end{bmatrix}
\end{aligned}\end{split}\]
\[\begin{split}\begin{aligned}
\underline{\underline{K}}_{\mathrm{b}i-\mathrm{c}i}^\Phi
\begin{bmatrix}
\delta \underline{u}_{\mathrm{b}i} \\
\delta \underline{\theta}_{\mathrm{b}i}\\
\delta \underline{u}_{\mathrm{c}i} \\
\delta \underline{\theta}_{\mathrm{c}i}
\end{bmatrix}
= \nonumber \\
\begin{bmatrix}
\underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}}\\
\underline{\underline{0}} & \mathrm{AX} \left(\underline{\underline{R}}_\mathrm{bi} \underline{\underline{R}}_\mathrm{pci}^T \underline{\underline{R}}_\mathrm{ci}^T \widetilde{\lambda}_{\mathrm{bi-ci},2} \right) &
\underline{\underline{0}} & \mathrm{AX2}\left( \underline{\lambda}_{\mathrm{bi-ci},2}, \underline{\underline{R}}_\mathrm{ci} \underline{\underline{R}}_\mathrm{pci} \underline{\underline{R}}_\mathrm{bi}^T\right) \\
\underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}}\\
\underline{\underline{0}} & -\mathrm{AX2} \left( \underline{\lambda}_{\mathrm{bi-ci},2}, \underline{\underline{R}}_\mathrm{bi} \underline{\underline{R}}_\mathrm{pci}^T \underline{\underline{R}}_\mathrm{ci}^T\right)
& \underline{\underline{0}} & -\mathrm{AX} \left( \underline{\underline{R}}_\mathrm{ci} \underline{\underline{R}}_\mathrm{pci} \underline{\underline{R}}_\mathrm{bi}^T \widetilde{\lambda}_{\mathrm{bi-ci},2} \right)
-\widetilde{\lambda}_\mathrm{ci-bi,1} \widetilde{ \underline{\underline{R}}_\mathrm{ci} \left( \underline{x}^\mathrm{r}_\mathrm{bi}-\underline{x}^\mathrm{r}_\mathrm{ci} \right) }
\end{bmatrix}
\begin{bmatrix}
\delta \underline{u}_\mathrm{bi} \\
\delta \underline{\theta}_\mathrm{bi}\\
\delta \underline{u}_\mathrm{ci} \\
\delta \underline{\theta}_\mathrm{ci}
\end{bmatrix}
\end{aligned}\end{split}\]
\[\begin{split}\begin{aligned}
\underline{\underline{K}}_\mathrm{nm-yb}^\Phi
\begin{bmatrix}
\delta \underline{u}_\mathrm{nm} \\
\delta \underline{\theta}_\mathrm{nm}\\
\delta \underline{u}_\mathrm{yb} \\
\delta \underline{\theta}_\mathrm{yb}
\end{bmatrix}
= \nonumber \\
\begin{bmatrix}
\underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}}\\
\underline{\underline{0}} & \mathrm{AX} \left(\underline{\underline{R}}_\mathrm{nm} \underline{\underline{R}}_\mathrm{yb}^T \widetilde{\lambda}_{\mathrm{nm-yb},2} \right) &
\underline{\underline{0}} & \mathrm{AX2}\left( \underline{\lambda}_{\mathrm{nm-yb},2}, \underline{\underline{R}}_\mathrm{yb} \underline{\underline{R}}_\mathrm{nm}^T\right) \\
\underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}}\\
\underline{\underline{0}} & -\mathrm{AX2} \left( \underline{\lambda}_{\mathrm{nm-yb},2}, \underline{\underline{R}}_\mathrm{nm} \underline{\underline{R}}_\mathrm{yb}^T\right)
& \underline{\underline{0}} & -\mathrm{AX} \left( \underline{\underline{R}}_\mathrm{yb} \underline{\underline{R}}_\mathrm{nm}^T \widetilde{\lambda}_{\mathrm{nm-yb},2} \right)
-\widetilde{\lambda}_\mathrm{nm-yb,1} \widetilde{ \underline{\underline{R}}_\mathrm{yb} \left( \underline{x}^\mathrm{r}_\mathrm{nm}-\underline{x}^\mathrm{r}_\mathrm{yb} \right) }
\end{bmatrix}
\begin{bmatrix}
\delta \underline{u}_\mathrm{nm} \\
\delta \underline{\theta}_\mathrm{nm}\\
\delta \underline{u}_\mathrm{yb} \\
\delta \underline{\theta}_\mathrm{yb}
\end{bmatrix}
\end{aligned}\end{split}\]
Note
The term \(\underline{\underline{K}}^\Phi\) is include here for
completeness, but is not in the current Kynema implementation, and
nonlinear-system convergence has been satisfactory.
Data layout
Tangent stiffness matrix
Sonneville, V., and O. Brüls. 2012. “Formulation of Kinematic
Joints and Rigidity Constraints in Multibody Dynamics Using a Lie
Group Approach.” In Proceedings of the 2nd Joint International
Conference on Multibody System Dynamics. Stuttgart, Germany.